منظور از Likelihood Ratio یا نسبت درست‌نمایی چیست؟

انتظار داریم که حرکت از بیمار به سمت بیماری، با شرح حال و معاینه فیزیکی شروع شده و از طریق استدلال بالینی به یک تشخیص پزشکی اولیه برسیم و سپس تست‌ها را برای تأیید یا رد تشخیص ارسال کنیم.

هر چند که مسیرِ واقعیِ رسیدن به تشخیص، بسیاری از اوقات طبق انتظار ما پیش نمی‌رود و بیماران با مجموعه‌ای از آزمایش‌ها و تصویربرداری‌های قبلی به دست ما می‌رسند.

یک مفهوم در این میان نیازمند توجه مضاعف است:

من اگر بیمار مسنی دارم که شرح حال درد قفسه سینه جدید می‌دهد و من به سندرم حاد کرونری شک کرده‌ام، چه تستی درخواست کنم؟ اصلاً چه سؤال دیگری بپرسم؟ چه معاینه‌ای انجام بدهم؟

• اگر گفت دردش فقط پنج ثانیه طول کشیده، باز هم به بیماری قلبی فکر کنم؟
• اگر گفت عرق می‌کند، چطور؟
• اگر فشار خونش طبیعی باشد، کمکی به تشخیص من می‌کند؟
• از وی نوار قلب بخواهم؟
• برای ایشان تروپونین درخواست کنم؟

و حتی سؤال را یک قدم سخت‌تر کنیم.

اگر تروپونین چک کردم و منفی بود، خیالم راحت بشود و بگویم مشکل قلبی نیست؟ اگر هم نوار و هم تروپونین منفی بود، چطور؟

برای جواب دادن به تمام سؤالات فوق باید با مفهوم likelihood ratio یا نسبت درست‌نمایی آشنا باشیم.

نسبت درست‌نمایی یا Likelihood Ratio چیست؟

فرض کنیم در جزیره‌ای به نام سالمان، ده هزار نفر زندگی می‌کنند. مردم سالمان زندگی نسبتاً خوبی دارند. آن‌ها عمدتاً رژیم غذایی حاوی ماهی و میوه‌های بومی جزیره را مصرف می‌کنند.

از آن‌جایی که آن‌ها به سلامتی خود بسیار اهمیت می‌دهند، دائماً بررسی‌های پزشکی برای خود انجام می‌دهند. محدودیتی نیز از نظر مسائل مالی ندارند.

از آن‌جایی که بیماری رایج در جزیره، حساسیت به نوعی خاص از نارگیل است، پزشکانِ سالمان به دنبال راهی برای تشخیص بهتر این بیماری هستند. متأسفانه این بیماری علامت اختصاصی خاصی نیز ندارد و مثل یک سرماخوردگی یا سینوزیت خود را نشان می‌دهد.

آن‌ها برای سال‌ها تمام مردم سالمان را مورد بررسی قرار داده و چهار شکایت و علامت زیر را در این بیماری که اسمش را نارگیلیت (Nargilitis) می‌گذاریم، بررسی کردند:

• خارش چشم
• قرمز شدن کف دست
• عطسه
• قرمز شدن نوک بینی

پزشکانِ سالمان به این نتیجه رسیدند که از هر ۱۰۰ بیمار مبتلا به نارگیلیت، ۹۰ نفر خارش چشم دارند. آن‌ها این شکایت را در افرادی که سالم بودند نیز بررسی کردند. از هر ۱۰۰ نفر سالم نیز، ۴۵ نفر از خارش چشم شکایت داشت. بالاخره در سالمان باد فراوان است و گرد و خاک و غبار به داخل چشم زیاد می‌رود و برای همین خیلی‌ها خارش چشم می‌گیرند.

با توجه به اعداد بالا، احتمال خارش چشم در فرد مبتلا به نارگیلیت ۰/۹ می‌شود و احتمال خارش چشم در فرد غیر مبتلا به نارگیلیت، ۰/۴۵ می‌شود.

حالا اگر این دو عدد را بر هم تقسیم کنیم، به یک نسبت می‌رسیم. ۰/۹ تقسیم بر ۰/۴۵ برابر با ۲ می‌شود. به این نسبت، نسبت درست‌نمایی یا likelihood ratio می‌گوییم.

نسبت درست‌‌نمایی یا likelihood ratio، نسبتِ احتمالِ یک یافته – در شرح حال، در معاینه، در آزمایش‌ها، در تصویربرداری‌ها و … – در فردی با یک بیماری خاص به احتمال یافتن آن در فرد فاقد آن بیماری است.

این عدد به ما چه می‌گوید؟

عطسه را در نظر بگیریم.

از هر ۱۰۰ نفر مبتلا به نارگیلیت ۶۰ نفر عطسه می‌زنند. از هر ۱۰۰ نفر غیرمبتلا به نارگیلیت نیز، ۶۰ نفر عطسه می‌زنند. پس احتمال در هر دو برابر با ۰/۶ است. نسبت احتمالات نیز در نتیجه (۰/۶ ÷ ۰/۶) برابر با یک می‌شود.

برای عطسه، likelihood ratio برابر با یک است. یعنی احتمال وجود داشتن عطسه در دو جمعیت مبتلا به نارگیلیت و غیرمبتلا به نارگیلیت برابر است. یعنی عطسه هیچ کمکی به من نمی‌کند که بگویم یک فرد نارگیلیت دارد یا ندارد. یعنی پرسیدن از عطسه حتی ضروری نیز نیست.

فرض کنیم likelihood ratio برابر با یک باشد. معنی آن چیست؟ یعنی در دو جمعیت این یافته برابر بود. پس هیچ کمکی به من نمی‌کند – نه در تأیید و نه در رد.

اما در مورد خارش چشم چطور؟ در خارش چشم، likelihood ratio برابر با ۲ بود. یعنی احتمال یافتن خارش چشم در افراد مبتلا به نارگیلیت دو برابر افراد غیر مبتلا به نارگیلیت است.

در حالت سوم فرض کنیم که قرمزی کف دست و قرمزی نوک بینی بررسی شده است.

از هر ۱۰۰ بیمار مبتلا به نارگیلیت، هر ۱۰۰ نفر قرمزی کف دست داشتند و هیچ کدام از ۱۰۰ نفر قرمزی نوک بینی نداشتند. از طرف دیگر هیچ کدام از صد فرد غیر مبتلا به نارگیلیت قرمزی کف دست نداشتند و تنها یک نفر قرمزی نوک بینی داشت.

احتمال قرمزی کف دست در نارگیلیت یک (صد در صد) و احتمال قرمزی نوک بینی در نارگیلیت صفر است. احتمال قرمزی کف دست در فرد غیر مبتلا به نارگیلیت صفر و احتمال قرمزی نوک بینی در فرد غیر مبتلا به نارگیلیت ۰/۰۱ است.

حالا likelihood ratio را حساب کنیم. LR برای قرمزی کف دست در نارگیلیت برابر (۰ ÷ ۱) یعنی بی‌نهایت است. یعنی اگر کسی قرمزی کف دست داشت، با علم فعلی‌مان، به قطع نارگیلیت دارد.

از طرف دیگر، LR برای قرمزی نوک بینی، برابر با صفر می‌شود (‍۱ ÷ ۰). پس اگر کسی قرمزی نوک بینی داشت، نارگیلیت ندارد. به عبارت دیگر، در افراد مبتلا به نارگیلیت انتظار نداریم قرمزی نوک بینی داشته باشند.

در دنیای واقعی، کم پیش می‌آید که LR صفر یا بی‌نهایت داشته باشیم. نزدیک به صفر و نزدیک به بی‌نهایت داریم که همان تست‌های gold standard ما هستند.

قسمت قابل توجهی از یافته‌های ما یک LR بین ۰/۱ تا ۱۰ دارند. بنابراین این‌جا یک موضوع دیگر نیز مهم می‌شود. قبل از این‌که به دنبال این یافته بگردم، چقدر احتمال می‌دادم که فرد فلان بیماری خاص را داشته باشد؟ همان مفهومی که به آن pre-test probability می‌گوییم.

عدد LR قرار است به ما بگوید که اگر فلان یافته وجود داشت یا وجود نداشت، احتمال قبل از تست (pre-test probability) ما چه تغییری خواهد کرد. به عبارت دیگر، وصل‌کننده‌ی pre-test به post-test probability، همین likelihood ratio است.

نوموگرام فاگان یا نوموگرام بیز

اگر من با توجه به اپیدمیولوژی و دیگر عوامل انتظار داشته باشم که یک فرد مسن با درد قفسه سینه، احتمالاً ۵۰ درصد سندرم حاد کرونری داشته باشد (عدد فرضی)، با یک تروپونین مثبت یا منفی، این احتمال چقدر تغییر می‌کند؟

فعلاً قرار نیست وارد جزئیات ریاضیات تشخیص (mathematics of diagnosis) بشویم. اما تمام این توضیحات را مدیون توماس بیز (Thomas Bayes) هستیم. قضیه بیز در مورد احتمال وقوع یک پدیده با توجه به شرایطی که روی آن اثر می‌گذارد صحبت می‌کند. مثلاً اگر تست تروپونین مثبت باشد (شرایط)، احتمال این‌که بیمار سکته قلبی کرده باشد (احتمال) چقدر است؟

در این درس به مباحث قضیه بیز نمی‌پردازیم. برای کاربردی کردن و قابل استفاده بودن در بالین، از نوموگرام فاگان کمک می‌گیریم که اقتباسی از قضیه بیز است. در سال ۱۹۷۵، دکتر Terrence J. Fagan مقاله‌ای سه پاراگرافی در New England Journal of Medicine چاپ کرد و نام خود را با Fagan Nomogram جاودانه کرد (+).

البته حدود ۴ دهه بعد این نمودار تغییراتی کرد و نمودار دو مرحله‌ای به وجود آمد که فعلاً نیازی به آن نداریم و با همان نمودار یک مرحله‌ای که از likelihood ratio استفاده می‌کند، جلو می‌رویم.

برای فهم بهتر به شکل زیر دقت کنید.

فرض کنید برای بیماری که مثال زدیم، تست تروپونین درخواست کرده‌ایم و مثبت شده است. فرض کنید LR تروپونین برای اینفارکت میوکارد برابر با ۵ باشد (این عدد فرضی است). با استفاده از این نوموگرام و اتصال اعداد ستون pre-test probability به LR و امتداد آن به ستون post-test probability، می‌توانیم احتمال وجود بیماری، پس از انجام آن تست خاص را متوجه شویم.

پس در این مثال فرضی، مثبت شدن تروپونین در کسی که ۵۰٪ احتمال داشت سندرم کرونری حاد داشته باشد، احتمال وجود بیماری پس از انجام تست را به حدود ۸۰٪ می‌رساند.

همان‌طور که در درس‌های قبلی گفته‌ایم، ایده‌آل این است که تست مورد نظر ما، post-test probability را به نزدیک صفر یا صد برساند؛ اما چنین تست‌هایی کم هستند.

محاسبه سریع احتمال پس از تست

آیا قرار است برای هر تست این نمودار را دم دست داشته باشیم و آن را به کار بگیریم؟

دکتر استیون مک‌گی (Steven McGee)، نویسنده‌ی کتاب کم‌نظیرِ Evidence-Based Physical Diagnosis در مقاله‌ی سال ۲۰۰۵ خود، یک روش ساده برای استفاده از likelihood Ratio معرفی کرده است.

کلینیسین باید LR را در ذهن خود در سه دسته جای بدهد:

• اگر LR = ۱ باشد، یعنی آن یافته در هر دو جمعیت به میزان یکسانی وجود دارد و در نتیجه کمک‌کننده نیست.
• اگر LR > ۱ باشد، یعنی آن یافته در جمعیت بیشتر بیشتر از جمعیت غیربیمار وجود دارد و هر چه این عدد بیشتر باشد، بهتر است. این‌جا تا بی‌نهایت می‌شود بالا رفت.
• اگر LR < ۱ باشد، یعنی آن یافته در جمعیت غیر مبتلا به آن بیماری خاصی، بیشتر یافت می‌شود و در نتیجه اگر یا این یافته وجود داشته باشد، احتمال بیماری کم می‌شود. کمترین حد LR صفر است. یعنی هیچ فرد مبتلا به آن بیماری خاص، چنین یافته‌ای ندارد.

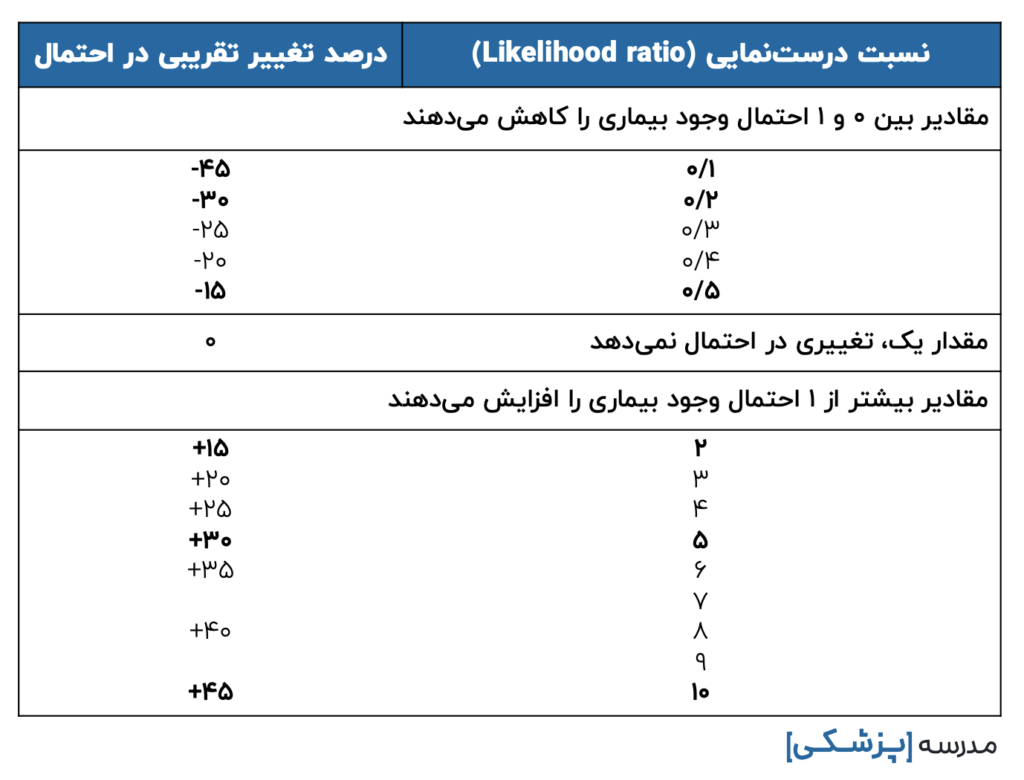
مک‌گی می‌گوید که برای LR کوچک‌تر از یک و بزرگ‌تر از یک، چند عدد خاص از آن‌ها را به خاطر بسپاریم:

• اگر LR = 2 باشد، احتمال را ۱۵ درصد زیاد می‌کند.
• اگر LR = 5 باشد، احتمال را ۳۰ درصد زیاد می‌کند (۱۵ درصد بیشتر).
• اگر LR = 10 باشد، احتمال را ۴۵ درصد زیاد می‌کند (۱۵ درصد بیشتر).

در مثال فوق، LR را ۵ فرض کردیم. در نتیجه احتمال قبل از تست را که ۵۰ بود، به ۵۰ + ۳۰ یعنی ۸۰ درصد تبدیل کرد.

برای LR کوچکتر از یک، معکوس سه عدد فوق را به خاطر بسپاریم:

• اگر LR = ۱ ÷ ۲ = ۰/۵ باشد، احتمال ۱۵ درصد کم می‌شود.
• اگر LR = ۱ ÷ ۵ = ۰/۲ باشد، احتمال ۳۰ درصد کم می‌شود.
• اگر LR = ۱ ÷ ۱۰ = ۰/۱ باشد، احتمال ۴۵ درصد کم می‌شود.

روش مک‌گی با تمام نقص‌هایی که دارد، بسیار در بالین کاربردی و سریع است و خوب به خاطر می‌ماند.

فراموش نکنیم که قرار نیست likelihood ratio راه حل نهایی تمام مسائل در پزشکی باشد. این ابزار نیز محدودیت‌هایی دارد. اما متأسفانه موقعیت‌های زیادی است که می‌توانیم از مفهوم likelihood ratio بهره‌ی فراوان ببریم و غافل می‌مانیم.

در درس‌های آتی بیشتر به likelihood ratio و محدویت‌های آن می‌پردازیم.

پیام درس و جمع‌بندی

تمرین درس

برای یکی از تست‌هایی که می‌شناسید، با جستجو و پیدا کردن منبع معتبر، likelihood ratio را در این‌جا بنویسید و بگویید در آن بیماری مد نظر شما، چه یافته‌ای LR بالاتر یا پایین‌تری دارد؟

منبع برای مطالعه بیشتر

دکتر Steven McGee از افرادی است که برای ترویج این مفاهیم و پزشکی مبتنی بر شواهد و روش علمی، زحمت فراوان کشیده است. سال ۲۰۰۵ وی مقاله‌ای با عنوان Simplifying Likelihood Ratios چاپ کرد. این مقاله کوتاه به درک بهتر این مفهوم بسیار کمک می‌کند. مقاله به رایگان از این لینک در دسترس است.